Flexion plane simple.
|
|
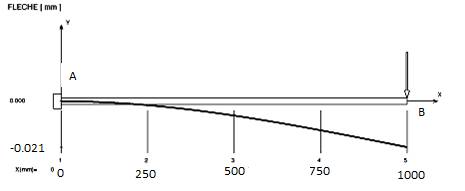
Etude d’un arbre de diamètre 35 en acier. E=210 000MPa, Re = 250MPa. Encastré en A.
Une étude logiciel donne les résultats indiqués par les courbes ci-contre.
A quel endroit se situe la flèche maximale ?
Quelle est la valeur de la flèche maximale ?
Quel est la valeur maximale de l’effort tranchant ?
Quel est la valeur maximale du moment fléchissant ?
A quel endroit se situe la contrainte maximale ?
L’arbre résiste-t-il ?
Quel est le coefficient de sécurité ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
Etude d’un arbre de diamètre 25 en acier. E=210 000MPa, Re = 250MPa. 3 appuis.
Une étude logiciel donne les résultats indiqués par les courbes ci-contre.
A quel endroit se situe la flèche maximale ?
Quelle est la valeur de la flèche maximale ?
Quel est la valeur maximale de l’effort tranchant ?
Quel est la valeur maximale du moment fléchissant ?
A quel endroit se situe la contrainte maximale ?
L’arbre résiste-t-il ?
Quel est le coefficient de sécurité ? |
|
|
|
|
|
|
|
|
|
|
|
P = 2000 daN.
AB/x=BC/x=CD/x=1m
Section : 25horizontalement et 200 verticalement.
a) Déterminer les réactions en A, B, C et D :
b) Déterminer les efforts tranchants les moments fléchissants dans le tronçon AB :
c) Déterminer les efforts tranchants les moments fléchissants dans le tronçon BC :
d) Déterminer les efforts tranchants les moments fléchissants dans le tronçon CD :
e) Tracer les diagrammes.
f) Déterminer le moment quadratique :
g) Déterminer la contrainte maximale :
Le MAP d’une liaison complète de deux pièces en plastique est réalisé à l’aide de languettes qui s’emboitent par déformation. La languette a une section rectangulaire de 1x5mm. Une force de 5 N est exercée verticalement. Le coefficient de sécurité est s=1,5.
A) Indiquer la sollicitation exercée sur la languette :
B) Repérer sur le schéma la zone la plus sollicitée.
C) Calculer le moment de flexion en cet endroit :
D) Calculer le moment quadratique de la section :
E) Déterminer la contrainte maximale :
F) Choisir le matériau adapté parmi ces trois :
|
Matière : |
PA 6/6 : Polyamide. |
POM : Polyoxyméthylène. |
PP : Polypropylène. |
|
Re : |
56 MPa |
98 MPa |
84 MPa |
|
E : |
1830 MPa |
2870 MPa |
1120 MPa |
G) Déterminer la flèche induite au montage :
Une courroie a besoin d’être tendue pour transmettre le couple, ce qui induit un effort non négligeable sur la poulie, et donc le palier qui assure la liaison pivot. L’arbre est en acier. Re = 150 MPa. Le coefficient de sécurité est de 3.
a) Indiquer la sollicitation exercée sur l’axe :
b) Calculer le moment de flexion au milieu du palier :
c) Ecrire la condition de résistance :
d) Déterminer le diamètre :
e) Déterminer la flèche induite :
|
Le système étudié est un moteur mécanique destiné à mouvoir un jouet
L’utilisateur agit sur le bouton de manœuvre 7 et remonte alors un ressort. Lorsque le jouet est mis en route, le ressort se détend et entraîne alors les pieds.
Pour permettre au bouton de remonter dans un seul sens le ressort, un système de roue libre est installé entre la tige de manœuvre 6 et la roue dentée 4 : double cliquet 1 et dents intérieures de la roue 4.
Lors du fonctionnement de la roue libre, le cliquet 1 se déforme. Cette déformation crée des sollicitations et donc des contraintes que vous devez identifier et quantifier pour valider (ou invalider) la conception de cette roue libre.
Le cliquet double est soumis à un effort de 3,2 N. Il est de section rectangulaire : 1x0,7mm et est considéré comme une poutre encastrée en B. Il est en POM : Re = 98 MPa. |
|
|
|
|
|
f) Isoler la poutre, appliquer le PFS et déterminer les actions mécaniques au point B :
g) En déduire les sollicitations dans le cliquet au point B :
h) Déterminer Mfz en B : |
|
i) Déterminer Igz :
j) Déterminer la contrainte de flexion :
Le tracé ci-dessous, issus du logiciel Cosmos Works, donne la valeur en tout point de la contrainte dans le cliquet.
k) Repérer la section la plus sollicitée.
l) Relever la valeur maximale de la contrainte.
m) Le matériau est-il résistant ?
n) Calculer le coefficient de sécurité.
o) Comparer la valeur obtenue par le logiciel et la valeur déterminée à la question et justifier la différence éventuelle par une représentation des contraintes :
|
|
|
